Research

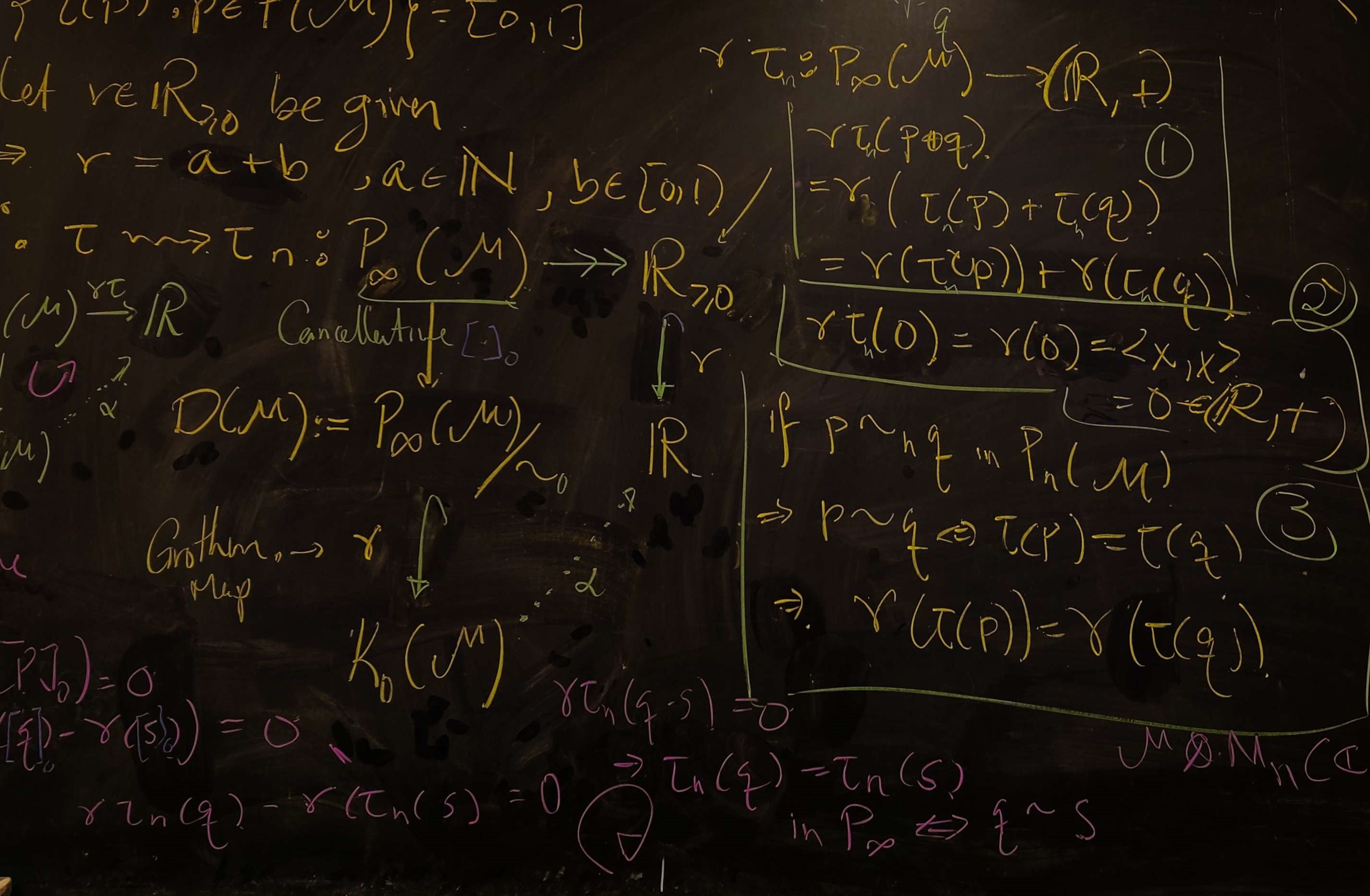
Elliott’s program to classify simple separable amenable \(C^*\)-algebras via K-theory and traces is now essentially complete modulo the necessary regularity assumptions of \(\mathcal{Z}\)-stability and the Universal Coefficient Theorem (UCT). This effort of some 50 years and many researchers was achieved most elegantly in the recent work of José R. Carrión, James Gabe, Christopher Schafhauser, Aaron Tikuisis and Stuart White, where it is shown that two unital full *-homomorphisms between two unital separable nuclear \(C^{*}\)-algebras \(A\), \(B\) where A satisfies the UCT and \(B\) is simple and \(\mathcal{Z}\)-stable are approximately unitarily equivalent if they agree on the total K-theory and trace invariant \(KTu(\cdot)\) This is equally well interpreted as the fact that two such maps are at zero approximate unitary distance on the unit ball of the source algebra. Our aim is to move beyond Elliott’s program and determine the distance between two such maps by developing a metric on the space of invariants \(KTu(\cdot)\) and demonstrating that the distance between the maps and invariants agree.

References

Carrión, J.R., Gabe, J., Schafhauser, C., Tikuisis, A. and White, S., 2023. Classifying \(^*\)-homomorphisms I: Unital simple nuclear \(C^*\)-algebras. arXiv preprint arXiv:2307.06480.